Solution to the hypercube problem
A four-dimensional hypercube has 32 edges. Here’s why. Start with a simple line segment. It has only one edge. We transform it into a square by copying it to a parallel line segment; its endpoints trace out two new edges, giving the four edges of a square: two copies of the original line segment (shown solid in the figure) plus two that are traced out by the endpoints of the line segment (shown dashed).

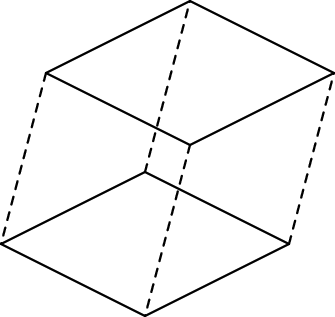
Next, we transform a square into a cube. We move the square to a parallel square to form a cube. As before, we get two copies of the square (original and parallel) giving 8 edges plus 4 more traced out by the corners of the square. The cube has 12 edges
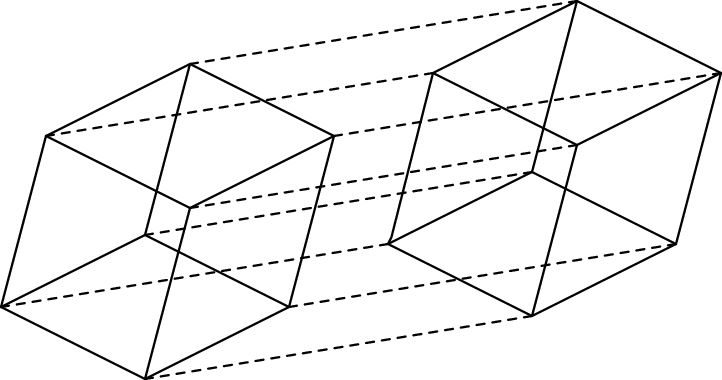
Now comes the leap into the fourth dimension. Just as before, we move the cube parallel to itself making two copies. That gives 12+12=24 edges. And, just as before, the 8 corners of the cube trace out an additional 8 new edges, for a grand total of 24+8=32 edges.